Big-O Notation

Big-O notation

• Worst-case analysis.
• Upper bound of an algorithm.
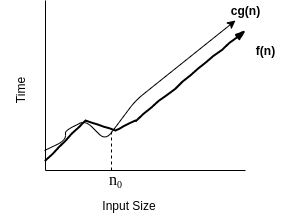
• O(g(n)) - {f(n) : there exist constants c and n₀ such that 0<=f(n)<=cg(n) for all n >= n₀}
• It is commonly used to calculate time analysis of an algorithm, it will give us an upper bound limit which doesn't exceed any input size. You can clearly see in the below diagram after a particular size of the input (n₀ ) after then the f(n) always lies in or below the c.g(n).

There are two basic rules for Big-Oh (0)

• Drop lower order term
• Drop constants

Let's understand the above rules in an example:-

     int a = 1; // O(1)
     int b = 2; // O(1)
     int c = 3; // O(1) 
     for (int i = 1; i <= n; i++) { // O(n + 1)
         for (int i1 = 1; i1 <= n; i1++) { // O(n +1)
             a = i*i1; // O(1)
             b = i*i1; // O(1)
             c = i*i1; // O(1)
         }
     }

    for (int i = 0; i < n; i++) { // O(n)
        a *= i; // O(1)
        b *= i; // O(1)
    }

    c = 0; // O(1)

We can say the running time T(n) = 3 + 3n² + 2n+ 1  = 3n² + 2n + 4, now we have to perform the above mentioned rule to get the time complexity.

• We are removing all the lower order terms from T(n) which will now become T(n) = 3n² + 4.
• Now, we have to perform the final steps to get the time complexity which we need to drop the constants after applying the 2nd rule T(n) will become O(n²).

According to our time complexity analysis, the above algorithm will never go beyond the O(n²) for any growth rate of input size.

Here are few commonly used function names in Big-O.

f(n)	Name	Example
1	Constant	Sum of Two number
log2n	Logarithmic	Binary Search
n	Linear	Kadane’s Algorithm
n*log2n	Log-Linear	Merge Sort
n2	Quadratic	Bubble Sort
n3	Cubic	Product of n*n matrix
2n	Exponential	Fibonacci