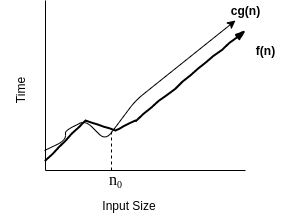
Big-θ (Big-Theta) Notation

When we use the big-θ notation bounds, a function from above and below; so it defines the exact asymptotic tight bound. Average case analysis. Tight bound of an algorithm. O(g(n)) - {f(n): there exist constants c1, c2 & n 0 such that 0<=c1.g(n) <= f(n) <= c2.g(n) for n>=n 0 }. Once n gets large enough, the running between c1.g(n) and c2.g(n). Let's understand it with the help of the program. private boolean searchValue( int [] n, int targetValue) { for ( int i = 0 ; i < n. length ; i++) { if (n[i] == targetValue) return true ; } return false ; } As per the above program, It will never go beyond the limit of θ(n) runtime analysis in the large value of n. There are two basic rule for Big-Theta (θ):- Drop lower order terms. Drop constants. If T(n) = 2n 2 + 2 then it will be 0 <= 2n 2 <= 2n 2 + 2 <= 3n 2 and it mean θ(n 2 ).