Counting Bits

-
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.
Input: 2
Output: [0,1,1]
Follow up:
  • It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?
  • Space complexity should be O(n).
  • Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.
Now, It is time to think before we write our code onto a paper. We read about the binary representation in college. A binary number is a special type of representation of a number in a binary format where the bit can be 0 or 1. You had an idea that the computer system also understands the 0's and 1's. 0's mean an inactive bit and 1's mean an active bit. Let's understand the easiest way to calculate the number using the pictorial diagram.
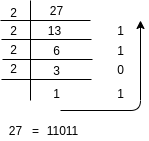
This is something that looks like 2's multiples and the remainder will go into the stack. When we pop the remainders from the stack it will look like the same as shown in picture 27 = 11011. 
Let's verify if the above binary digit is equal to the number or not with the help of binary to decimal conversion.
27 = 1*24 + 1*23 + 0*22 + 1 * 21 + 1 * 20
This is the process of binary representation numbers.
Our problem statement is a bit similar but we need to just count only the active bits (1) for each number 0 to num which will be passed by the user.
If you observe the above chart then you come to know that there is some pattern which follows that every certain number drops to 1. If you look more into the pattern it will help us to resolve from the bottom-up approach. This graph gives us more information, if you look into the graph 2, 4, 8, 16 all 1 which means that 4/2 = 2. For an even number, you can directly fetch half of the number 1's count. For an odd number, it will fetch half of the number 1's count + 1.

Number012345
1’s count011212
Let's do the code and understand it in deep-dive
public static int[] countBits(int num) {
    int[] resultBit = new int[num+1];
    resultBit[0] = 0;
    for (int i = 1; i < num+1; i++) {
        if (i%2 != 0)
            resultBit[i] = resultBit[i/2] +1;
        else
            resultBit[i]=resultBit[i/2];
    }
    return resultBit;
}
I hope you are understanding the solution to the given problem. We will come up with a new challenge soon.

Comments

Post a Comment

Popular posts from this blog

Recursion

-
Image
The process in which a function calls itself and only works where we call the same operation multiple times with different inputs. In every call, we try to make the problem smaller. There must be a base case where the system will stop the recursion and give you a result back. It internally stores the recursion state in the method call stack. If there is no base condition in the recursion method then it will go into an infinite loop and you might face the StackOverflow Exception . There are several types of recursion:- Head Recursion Tail Recursion Tree Recursion Nested Recursion Head Recursion It will call recursively first then at the end do all the computation. private static int factorial( int number) { return (number== 1 )? number : number* factorial (number- 1 ) ; } factorial(5) (5* factorial(5-1)) (5* (4* factorial(4-1)) (5* (4* (3*factorial(3-1))) (5* (4* (3* (2*factorial(2-1)))) (5* (4* (3* (2* (1*1))))) output = 120 Tail Recur...
Read more

Stack

-
Image
The Stack  looks more like a container which holds the element, will insert element from the top and remove from the top only. It follows the Last in First out(LIFO)  or First In Last out (FILO)  approach. Java uses the method stack area to hold the state of the method if some method calls another method inside it.   public class Demo { public static void main(String[] args) { new Demo().firstCall(); System. out .println( "Main" ); } public void firstCall() { secondCall(); System. out .println( "First" ); } private void secondCall() { thirdCall(); System. out .println( "Second" ); } private void thirdCall() { System. out .println( "Third" ); } } This is how it maintains the method call in the method stack area. It will remove from the top every time and complete its method execution and remove next's top from the stack. This process will continue until th...
Read more

Data Structure & Algorithm

-
Image
I am going to start the complete data structure and algorithm blog series to help the developer community understand the basics and help them become more productive in their work environment. As we all are under lockdown until the next update from the government, I have decided to support my friends and colleague to understand the data structure and algorithm. Let's begin by separating the data structure and algorithm in two terms. When you hear about data structure,  what comes first to your mind. I believe most of you thought of storing any form of data in an efficient way. Yes, You are correct 👍. Now, Second and the most important term is an algorithm , It is a set of rules to be followed to solve a problem. To gain more understanding of the data structure and algorithm, let us take an example:- E.g., We are all going to attend the google conference and they have a single registration desk. If we all reach the registration counter together, to register ourselves. Such a ...
Read more