Queue

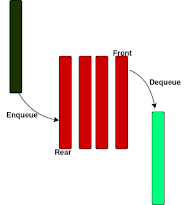
A Queue is a data structure that holds the element, will insert from the rear of the queue, and remove from the front of the queue. Insertion is known as Enqueue and Deletion is known as Dequeue. It follows the First In First Out(FIFO) or Last In Last out(LILO). There are many problem statements where we generally use the queue to hold the object and process it whenever it is required. One of the most used application is RabbitMq in real-time projects. Let's take an example, there are 1 publisher and 1 subscriber, publisher publish an object into the queue, and the subscriber will subscribe and remove it from the queue. We can implement a queue using an Array or Linked List. 

                                                              

NOTE: -Generic <T> type can accept any data type, If you have not passed explicitly then it will consider it as an Object.

Queue Implementation using Array

#1 Initialization of Custom Queue

public class CustomQueue<T> {
    T[] data;
    Integer length = 0, capacity = null, front = 0, rear = -1;

    public CustomQueue(T[] data) {
        this.data = data;
        capacity = data.length;
    }

}

#2 Enqueue an element

public void enqueue(T ele) {
    if (ele == null)
        throw new NullPointerException();
    if (length < capacity) {
        rear = (rear + 1) % capacity;
        data[rear] = ele;
        length++;
    }else
        throw new IllegalStateException();
}

In the above code, we are calculating the next insertion index based on the current (rear + 1) mod capacity. This could be an easy way to calculate it and enqueue it in the right place. If we dequeue an element from the queue then we have to remove the front element and move one by one all element towards left. This whole process will consume O(n) time complexity to complete it. To overcome this problem, we are moving our front to (front+1) mod capacity. It is an easy and best way to put the element in the right position without any overburden to shift elements towards left in the dequeue program.

#3 Dequeue an element

public void dequeue() {
    if (length == 0)
        throw new NoSuchElementException();
    else {
        front = (front + 1) % capacity;
        length--;
    }
}

#4 Peek an element

public T peek() {
    if (length != 0)
        return data[front];
    throw new NoSuchElementException();
}

#5 Printing elements

private void print() {
    if (front > rear) {
        for (Integer integer = front; integer < capacity; integer++) {
            System.out.print(data[integer] + " ");
        }
        for (Integer integer = 0; integer <= rear; integer++) {
            System.out.print(data[integer] + " ");
        }
    } else {
        for (Integer integer = front; integer < rear + 1; integer++) {
            System.out.print(data[integer] + " ");
        }
    }
}

In the above code, we have to be very careful while traversing in a queue. There are some cases when the rear reference is reached the last index of an array and the front reference is not in the first position of the array then the next value will going to be inserted in the 0th index until capacity is full. This is kind of the rotate insertion of an array.

Queue Implementation using Linked List

#1 Initialization of Custom Queue

public class CustomQueue<T> {
    class Node<T> {
        T data;
        Node next;

        public Node() {
        }

        public Node(T data) {
            this.data = data;
        }

        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
    }

    Node<T> front, rear;
    Integer length = 0;
}

#2 Enqueue an element

public void enqueue(T ele) {
    if (ele == null)
        throw new NullPointerException();
    if (rear == null) {
        front = rear = new Node<T>(ele);
    } else {
        rear.next = new Node<T>(ele);
        rear = rear.next;
    }
    length++;
}

#3 Dequeue an element

public void dequeue() {
    if (front == null)
        throw new NoSuchElementException();
    front = front.next;
    length--;
}

#4 Peek an element

public T peek() {
    if (front != null)
        return front.data;
    throw new NoSuchElementException();
}

#5 Printing elements

public void print() {
    Node<T> ref = front;
    while (ref != null) {
        System.out.print(ref.data + " ");
        ref = ref.next;
    }
}

If you have noticed, the implementation of the queue using a linked list. We are not bound with the size limit. We can add n number of the element and remove it in constant time. I hope you understand the logic behind it.